English
Pragelato è il luogo dove tradizionalmente da ormai 9 anni si svolge lo Stage di Matematica ovvero una tre giorni intensiva di lavoro matematico con allievi delle prime quattro classi delle Scuole Superiori.
E’ difficile rendere solo a parole il clima che si respira durante lo Stage di Matematica, risulta sempre incredibile che dei ragazzi possano lavorare per così tante ore consecutive sulla matematica: eppure è così.
I numeri parlano chiaro ed indicano un sempre maggiore interesse per l’iniziativa.
Quest’anno ben 900 allievi, suddivisi in 5 gruppi hanno partecipato allo Stage di Matematica, allievi provenienti principalmente da Licei Scientifici, ma anche da Licei Classici, Licei Linguistici ed Istituti Tecnici.
Con la visuale dell’insegnante i punti di forza dell’iniziativa sono:
- l’interazione produttiva tra energie diverse: l’Università (con il prof. F. Arzarello, il prof. M. Albano, il prof. F. Pastrone) ed i laureandi ad indirizzo didattico; la S.I.S con alcuni supervisori ed un nutrito numero di specializzandi; i docenti e gli allievi della Scuola Superiore, a turno tutti con un ruolo da protagonista per illustrare in modo approfondito i concetti più complessi (conferenze sui Numeri Trasfiniti di Cantor, su Teoria del Caos, sulla Teoria dei Nodi) o per animare i giochi matematici, oppure per presentare con modalità inconsuete tematiche legate ai vari argomenti trattati.
- L’ambiente naturale in cui si opera: gli allievi infatti lavorano per lo più in spazi aperti ed in qualche occasione( es. l’analisi dell’esperienza di Talete sulla misurazione dell’altezza di una piramide) trovano subito gli elementi adatti a vagliare quanto viene loro proposto (es. come si modifica l’ombra della piramide stessa alle varie ore del giorno).
- Lo spirito di collaborazione di un nutrito gruppo di docenti che mettono in comune le loro idee, che preparano minuziosamente le varie attività dello Stage in numerosi incontri che si tengono di martedì a Palazzo Campana.
Nel lavoro dei docenti, spesso all’esperienza di chi ha già molti anni di insegnamento si affiancano l’effervescenza, la fantasia, le nuove abilità di docenti più giovani e da questa unione nascono le idee migliori.Tra le tante vorrei segnalare l’esperienza con l’origami per la costruzione di poliedri stellati, l’utilizzo dell’inversore sulla scacchiera della dama per verificare che effettivamente un piccolo cerchio può “racchiudere” tutta la parte di piano che sta intorno alla scacchiera, il biliardo ellittico per verificare le proprietà dei due fuochi di un’ellisse.
- I contenuti insoliti: una matematica con radici storiche ma proiettata a far capire applicazioni o tematiche di grande attualità.
- Le modalità di studio: una ricerca personale di significati su una traccia appena abbozzata da un fascicolo di lavoro.
- Il supporto al ragionamento dato dai materiali concreti da manipolare ed utilizzare talvolta solo per un pretesto di gioco, ma altre volte per una visione più efficace e convincente.
Ci sembra a questo punto molto pertinente quanto affermava J. Piaget (nel testo ” Dove va l’educazione?):
“Si insegna la matematica come se si trattasse esclusivamente di verità accessibili per mezzo di un linguaggio astratto, anzi, di quel linguaggio particolare che si serve di simboli operativi: ora, la matematica consiste, in primo luogo e sopra tutto, nelle azioni che vengono esercitate sulle cose, e le stesse operazioni sono pur sempre delle azioni, ma ben coordinate tra di loro e semplicemente immaginate invece di essere eseguite materialmente. Indubbiamente è indispensabile arrivare all’astrazione, anzi ciò è del tutto naturale in qualunque campo, nel corso dello sviluppo mentale dell’adolescenza. Ma l’astrazione non è che una specie di inganno e di deviazione mentale se non costituisce il punto di arrivo di una serie ininterrotta di azioni concrete anteriori. La vera causa degli insuccessi dell’educazione formale dipende dunque essenzialmente dal fatto che si incomincia con il linguaggio (….) invece di incominciare con l’azione reale e materiale.
Ecco, allo Stage si tende ad incominciare con l’azione reale e materiale.
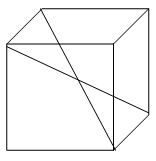Significativa a questo proposito è la questione che noi poniamo agli allievi su come si presentano tra loro due diagonali di un cubo.
E’ facile cadere in inganno e credere che siano tra loro perpendicolari. Basta invece sollevare la faccia superiore di un cubo in cartoncino, disporre due bastoncini a rappresentare le diagonali per accorgersi che i quattro vertici uniti dalle due diagonali formano un rettangolo e da questo dedurre che le diagonali di un cubo non possono essere tra loro perpendicolari poiché non possono esserlo le diagonali di un rettangolo.
Può essere convincente anche infilare un bastoncino a collegare due vertici opposti e simulare così una delle diagonali del cubo e far ruotare velocemente il cubo intorno ad esso: ciò che si ottiene è inaspettato e non solo prova che due diagonali di un cubo non sono tra loro perpendicolari ma si può rimandare a nuove ed interessanti questioni.
Ma che cosa pensano i ragazzi di tutto ciò?
Lasciamo parlare i protagonisti dell’iniziativa e per tutti riportiamo quanto scritto da un gruppo di allievi di I liceo a proposito del lavoro su ” Magia? No! Soltanto matematica”
Questa esperienza ci è stata amica come solo i numeri sanno esserlo, abbiamo giocato insieme (a scacchi con il Visir), abbiamo mangiato insieme ( milioni di miliardi di chicchi), con la magia che ci avete insegnato vi abbiamo fatti sparire e ricomparire, o cari Professori; in questo viaggio su una nave lontana dalle coste del nostro Liceo, abbiamo imparato a essere, oltre che vostri affezionati alunni vostri amici come 9437056 lo è con 9563584.
Se volete qualche delucidazione su queste affermazioni rimane valido ancora l’invito già altre volte formulato di venire a vedere di persona ciò che accade a Pragelato.