Materiali Classe II

Il percorso è suddiviso in attività che portano al concetto di infinito dal punto di vista aritmetico o dal punto di vista geometrico..

Le attività spesso presuppongono l’utilizzo di materiale concreto.
I ragazzi/e lavorano sempre in gruppo ed   in ciascun gruppo sono presenti tutti i materiali utili al lavoro.

Si parte da una serie di domande sul concetto di infinito: all’interno del gruppo devono giungere ad una risposta comune che viene poi riportata su appositi fogli poi esposti lungo un filo rosso che taglia l’aula di lavoro.

A questo stesso filo rosso verrà poi anche appeso il cartellone creato da ciascun gruppo al termine dei tre giorni di lavoro e che evidenzierà le nuove conclusioni a cui sono pervenuti i ragazzi/e dopo le esperienze vissute.
Il cartellone migliore dal punto di vista dei contenuti costituirà la copertina del fascicolo dell’anno successivo.

Si passa poi ad una attività di suddivisione di torte di carta che porta al concetto di serie ed alla formula relativa alla somma di serie geometriche.

I risultati vengono costruiti dagli allievi/e attraverso le attività e quindi spesso non sono univoci né definitivi:  per tutto il percorso spesso ritornano sui risultati ottenuti e tendono a “correggere” le loro prime certezze.

La formula relativa alla somma di serie geometriche viene inizialmente accettata dopo aver generalizzato alcuni casi su cui si è lavorato: si evidenzia così che matematicamente questa metodologia non è corretta e che ogni proprietà necessita di “dimostrazione”: la congettura di Goldbach evidenzia la pericolosità di trarre conclusioni affrettare.
Il percorso si chiude con una suddivisione di torte vere che i ragazzi/e delle classi II hanno portato da casa.

Attraverso un gioco di gruppo  e attraverso la costruzione di un grande domino si crea una metafora del procedimento di dimostrazione per induzione e se ne evidenziano le caratteristiche per applicarle poi su un caso concreto:  la somma di n numeri dispari.

Circa la formula relativa alla somma di una serie geometrica, si evidenziano i passi necessari per giungere alla dimostrazione e la si lascia in sospeso.

Si passa ad analizzare la questione della corsa tra Achille e la tartaruga 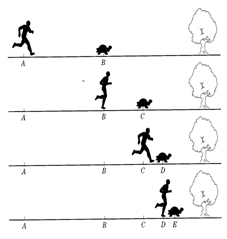per passare a parlare di numeri periodici.

Si considera la questione relativa a 0,(9).
La trasformazione in frazione viene analizzata da più punti di vista, anche attraverso percorsi originali trovati negli anni dai ragazzi/e.
Proprio attraverso il passaggio da scrittura periodica a frazione, analizzato su numeri scritti in basi diverse si giunge a dimostrare rigorosamente la formula relativa alla serie geometrica.

Tornando così ad Achille e la tartaruga si ha la possibilità di analizzare i singoli calcoli e di convincersi anche attraverso questi che Achille effettivamente potrà raggiungere e superare l’avversaria.

Attraverso situazioni di gioco, si rilanciano altre questioni relative all’infinito considerando la serie armonica, le questioni sollevate da Galileo, i “problemi” di Hilbert.

In questo caso, sottoposte le questioni agli allievi/e si portano gli allievi sulle idee di Cantor e sui numeri Trasfiniti attraverso una lezione partecipata oppure attraverso una conferenza tenuta da un docente dell’Università.

Si passa quindi ad analizzare l’infinito nell’arte attraverso alcune delle opere di M.C. Escher per soffermarci sull’opera “Limite del quadrato”.

Ci si sofferma poi sulla misura della diagonale di un quadrato ottenuta applicando il teorema di Pitagora e considerando i lati di misura unitaria: si affronta perciò la questione dei numeri irrazionali e viene proposta una dimostrazione della irrazionalità di  attraverso ”la discesa infinita”

Con una digressione storica si analizza il metodo babilonese relativo al calcolo della radice quadrata di un numero e lo si propone attraverso l’utilizzo degli strumenti di oggi, cioè delle calcolatrici.

Si introducono le frazioni continue come metodo per “imbrigliare” l’infinito partendo dallo “Spettro di un numero razionale” calcolato geometricamente su un rettangolo i cui lati hanno come misura il numeratore ed il denominatore di una frazione.
Si calcola così lo spettro di  sempre per via geometrica per scoprire una sorprendente ripetitività. In tutte queste attività gli allievi/e sono sollecitati ad utilizzare le calcolatrici in modo costruttivo e ragionato.

Si analizzano i formati della carta, prima il formato A4 e poi il formato aureo. Ci si sofferma così sulla sezione aurea, sui triangoli aurei con attività anche di origami. Si costruisce la spirale logaritmica.

Come ultima questione riguardante l’infinito si introduce la curva di Peano attraverso una collaborazione all’interno del gruppo e poi tra i vari gruppi: ciascun gruppo costruisce un livello di una curva di Peano, i vari tasselli vengono poi assemblati insieme per creare il livello successivo.

Si riprendono le carte di cioccolate Kinder che sono state distribuite il primo giorno, come supporto per la risoluzione di un problema, e, poiché il loro formato è 1:  si costruiscono con la tecnica dell’origami dei tetraedri. Con la collaborazione di un gran numero di allievi si giunge a costruire un tetraedro di Sierpinsky, che chiude il nostro percorso.