Materiali Classe III

Comunicare senza farsi capire: la crittografia.

Definita la crittografia, si segue un percorso storico costruendo di volta in volta gli oggetti (scitale, griglie, dischi)

Viene analizzato:
il cifrario di Cesare;
il disco di Alberti,
il cifrario monoalfabetico casuale
il cifrario polialfabetico,
la griglia di Vigenère
il  test di Kasiski.

Si passa poi ad analizzare i legami tra crittografia e matematica introducendo le classi di resto, le operazione nelle classi di resto e le relative proprietà.

Parlando di potenze nell’aritmetica modulare si definisce la funzione di Eulero, se ne studiano le proprietà e la si applica nella risoluzione di equazioni diofantee.

Si conclude  presentando il sistema RSA che viene poi applicato per spigare il sistema di sicurezza del bancomat.

In calce gli allievi possono trovare materiali di approfondimento su:
la regina Maria Stuarda
la decifrazione delle lingue morte
la macchina Enigma
i cifrari degeneri.

L’attenzione e l’impegno degli allievi/e viene mantenuta alta anche utilizzando i vari esercizi come possibilità di punteggio per la Caccia al tesoro.

Proposta di lavoro per il percorso sui Solidi Platonici (Classi III)

Seguendo le istruzioni costruite 12 moduli e poi assemblateli.
Potete anche consultare il sito.
http://www.nickrobinson.info

Osservate  un modulo:

Con 12 moduli avete costruito un rombododecaedro

• Perché questo nome?
• Quante facce ha?
• È un solido regolare? Perché?
• Che cosa accade nei suoi vertici?
• Con delle steccoline evidenziate gli angoloidi. Che cosa osservate?

Il rombododecaedro è  un solido con 12 facce a forma di rombo, ma rombi un po’ particolari. Se la diagonale minore vale 1, la diagonale maggiore vale … e anche i lati potete calcolarli da soli:

spigolo rombododecaedro = …

Per rispondere a queste domande potete trovare suggerimenti osservando attentamente uno dei moduli che avete costruito con gli origami.

Che formato hanno i foglietti con cui avete costruito i moduli?

Dimostrate che il rombo ottenuto al centro del vostro modulo ha proprio sulle diagonali le relazioni che avete prima evidenziato.

Che volume avrà il rombododecaedro?
Domanda difficile? non proprio, ma forse si potrà rispondere facilmente tra un po’!
Se ancora avete difficoltà a trovare una formula per calcolare il volume del rombododecaedro vi proponiamo di lasciarlo in sospeso e di analizzare il quesito successivo che potrebbe fornirvi qualche idea.
Il rombododecaedro è la forma che le api hanno dato al fondo delle loro cellette.
Se le api economizzano su tutto,  calcolate il loro risparmio nel lavorare con un fondo a forma di rombododecaedro.
Per semplicità immaginate di avere un volume di miele pari a 2 cm³.
Pensate ora di doverlo racchiudere in un cubo: quanta cera occorre per le pareti? (ovvero quanto misura la sua area totale?

Se invece il contenitore fosse a forma di rombododecaedro, quanta cera occorrerebbe?

Tuttavia le api sicuramente non sanno calcolare, quindi la forma a”tetto rombico” delle cellette pur essendo il più economico ed il più resistente deve dipendere da altri fattori.

Vediamo di capire con una attività:
Con della plastilina o del pongo  comporre 4 sfere del diametro di circa 3 cm. Disporre le sfere a tetraedro, cioè collocarne tre a triangolo e poi nell’incavo adagiare l’ultima sfera.

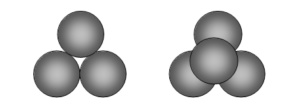Ora premete via via su due  facce in modo uniforme cercando di spingere le sfere ad aderire tra loro.
Completata l’operazione sollevate la sfera superiore e noterete …

Questo spetta a voi perché l’apprendimento è molto condizionato dalla capacità di meravigliarsi e ci si può meravigliare  solo su fatti inaspettati, quindi non svelati prima dal docente.

(testo di Gemma Gallino)