Il percorso è suddiviso in attività che portano a conoscere concetti matematici presenti in molti strumenti utilizzati quotidianamente e ad indagare al di là dell’applicazione, come si giunge correttamente a costruire idee matematiche.
Dopo una breve presentazione generale dell’iniziativa e delle regole di base di comportamento, gli allievi/e partecipano in gruppo ad un “gioco” che sa di magia: insieme scelgono un numero tra 1 e 63, i docenti attraverso l’utilizzo di alcune tabelle sono in grado di indovinare il numero scelto.
Gli allievi/e sono condotti così a capire su che cosa si basa il gioco e come sono costruite le tabelle. Si costruiscono così un kit di schede personali estendendo le loro possibilità di scelta su numeri maggiori.
L’analisi delle schede porta a considerare le idee del primo “gigante” sulle cui spalle è utile disporsi per poter vedere più lontano: si tratta di Leibniz e della sua idea del sistema binario per la scrittura dei numeri.
Gli allievi vengono poi guidati alla costruzione di due “macchine” in grado di semplificare l’operazione di cambio di base nella scrittura dei numeri e vengono evidenziate situazioni in cui viene utilizzata la base due nella scrittura dei numeri.
Il computer così apre alcuni dei suoi segreti e viene analizzato il codice Ascii per scrivere parole e simboli, evidenziando sempre su quali spalle è stato importante salire per giungere all’idea definitiva: il codice Morse, il codice Baudot.
Per il codice Morse viene presentato un piccolo circuito elettrico capace di riprodurre linea e punto e viene poi evidenziata l’idea geniale di Morse, che è stata quella di pensare di poter “allungare” il filo.
Relativamente al codice Baudot vengono colte anche suggestioni diverse provenienti da situazioni che sembrerebbero non avere nulla a che fare con la matematica: infatti il complesso musicale Coldplay ha utilizzato il codice Baudot per scrivere il titolo di un loro album.
Nel percorso alla ricerca di spalle di giganti si parla di George Boole per il suo contributo al “calcolo logico” che, ripreso da C. Shannon, trovò applicazione nei circuiti elettronici e quindi nei computer.
Analizzando un diagramma di flusso in cui si chiede lo scambio di dati, attraverso un gioco collettivo si simula ciò che accade all’interno del computer.
Considerato che tutti gli strumenti informatici registrano i dati attraverso stati elettrici, ci si pone il problema di come possano questi strumenti funzionare bene, anche quando presentano qualche anomalia. Si introducono, sempre attraverso un gioco, i codici a correzione d’errore.
I giganti in questo caso sono Fano ed Hamming.
 Alcuni giochi coinvolgono gli allievi/e ad analizzare i Codici a barre e ad affrontare la matematica che ne giustifica il funzionamento.
Alcuni giochi coinvolgono gli allievi/e ad analizzare i Codici a barre e ad affrontare la matematica che ne giustifica il funzionamento.
Considerando l’ipotesi futura di computer “Ternari”, attraverso un gioco con le carte si introduce la scrittura dei numeri in base tre seguendo la proposta di un antico problema babilonese sull’utilizzo di pesi per una bilancia.
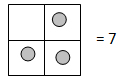 Alla ricerca di giganti che si sono occupati scrittura dei numeri e di “Macchine per calcolare” si analizza l’abaco introdotto da G. Papy e con questo ci si cimenta in calcoli complessi come divisioni e moltiplicazioni.
Alla ricerca di giganti che si sono occupati scrittura dei numeri e di “Macchine per calcolare” si analizza l’abaco introdotto da G. Papy e con questo ci si cimenta in calcoli complessi come divisioni e moltiplicazioni.
Si considera un metodo Babilonese per eseguire moltiplicazioni ed il metodo degli Egizi per moltiplicazioni e divisioni.
Gli Egizi poi offrono spunti matematicamente rilevanti a proposito della scrittura delle frazioni: nel nostro percorso, attraverso giochi collettivi si giunge a costruire alcuni dei metodi utilizzati dagli scribi per scrivere frazioni come somma di frazioni unitarie.
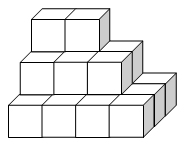 Utilizzando particolari piramidi formate da cubetti unitari, si pone agli allievi/e il problema di determinare il numero di cubetti che possono formare una piramide di npiani.
Utilizzando particolari piramidi formate da cubetti unitari, si pone agli allievi/e il problema di determinare il numero di cubetti che possono formare una piramide di npiani.
Alla ricerca di “giganti”che hanno sperimentato il fatto che una immagine o un oggetto possano essere di notevole aiuto per capire e risolvere problemi si incontra Pitagora e si lavora con numeri quadrati, con numeri gnomone e si affronta con queste immagini il calcolo di una radice quadrata o la determinazione di una formula per somare i numeri pari da 1 a 2n.
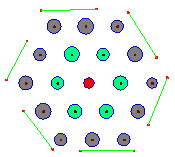 Sempre attraverso l’esempio di precedenti “giganti” si analizzano alcune problematiche proposte da Martin Gardner risolte con una raffigurazione geometrica dei numeri: si tratta dei numeri esagonali.
Sempre attraverso l’esempio di precedenti “giganti” si analizzano alcune problematiche proposte da Martin Gardner risolte con una raffigurazione geometrica dei numeri: si tratta dei numeri esagonali.
Si giunge a costruire la formula per ottenere la somma dei successivi numeri esagonali, ma si utilizzano anche numeri triangolari, presentando la vicenda di Gauss da bambino e del compito che gli era stato assegnato di calcolare la somma di tutti i successivi numeri naturali da 1 a 100.
In questo caso i materiali utilizzati permettono agli allievi/e di scoprire da soli molte proprietà.
Il passaggio da un personaggio e l’altro viene introdotto da giochi su labirinti e da costruzioni con origami.
Il percorso si conclude con una serie di giochi-problemi collegati con i concetti appresi: tutto viene proposto come un allenamento per la Caccia al tesoro che si svolge nell’ultimo pomeriggio dello Stage e che rappresenta il momento valutativo.
 Nella storia di ogni studente ci sono basi assolutamente da mettere se si vuole andare lontano: forse non si tratta di arrampicarsi sulle spalle di giganti ma si può pensare ad un piccolo piedestallo su cui appoggiarsi per poter vedere qualcosa.
Nella storia di ogni studente ci sono basi assolutamente da mettere se si vuole andare lontano: forse non si tratta di arrampicarsi sulle spalle di giganti ma si può pensare ad un piccolo piedestallo su cui appoggiarsi per poter vedere qualcosa. Davvero non era semplice: ed allora che cosa è accaduto?
Davvero non era semplice: ed allora che cosa è accaduto?


 English
English
 Si può amare la musica soltanto con anni di studio sul solfeggio?
Si può amare la musica soltanto con anni di studio sul solfeggio? Alcuni giochi coinvolgono gli allievi/e ad analizzare i Codici a barre e ad affrontare la matematica che ne giustifica il funzionamento.
Alcuni giochi coinvolgono gli allievi/e ad analizzare i Codici a barre e ad affrontare la matematica che ne giustifica il funzionamento. Alla ricerca di giganti che si sono occupati scrittura dei numeri e di “Macchine per calcolare” si analizza l’abaco introdotto da G. Papy e con questo ci si cimenta in calcoli complessi come divisioni e moltiplicazioni.
Alla ricerca di giganti che si sono occupati scrittura dei numeri e di “Macchine per calcolare” si analizza l’abaco introdotto da G. Papy e con questo ci si cimenta in calcoli complessi come divisioni e moltiplicazioni. Utilizzando particolari piramidi formate da cubetti unitari, si pone agli allievi/e il problema di determinare il numero di cubetti che possono formare una piramide di npiani.
Utilizzando particolari piramidi formate da cubetti unitari, si pone agli allievi/e il problema di determinare il numero di cubetti che possono formare una piramide di npiani. Sempre attraverso l’esempio di precedenti “giganti” si analizzano alcune problematiche proposte da Martin Gardner risolte con una raffigurazione geometrica dei numeri: si tratta dei numeri esagonali.
Sempre attraverso l’esempio di precedenti “giganti” si analizzano alcune problematiche proposte da Martin Gardner risolte con una raffigurazione geometrica dei numeri: si tratta dei numeri esagonali.